Matematica e musica sembrerebbero due ambiti molto distinti tra loro. In realtà hanno diversi punti in comune, come si può evincere già dalla loro definizione (tratta da Wikipedia):
- MATEMATICA: disciplina che studia le quantità, lo spazio, le strutture e i calcoli.
- MUSICA: arte dell’organizzazione dei suoni nel tempo e nello spazio.
Notiamo che la parola spazio si trova in entrambe le definizioni, così come organizzazione e struttura, che risultano essere due concetti strettamente correlati. Spazio, struttura ed organizzazione sono degli elementi che il linguaggio della matematica descrive in modo puntuale e rigoroso, ma il loro utilizzo viene sfruttato anche nell’ambito artistico così come nella musica.
SUONI ARMONICI
Uno dei fenomeni più significativi nella musica è quello dei suoni armonici: ogni suono contiene in sé infiniti altri suoni (frequenze) che, combinandosi assieme in dosi ed intensità diverse, ci fanno percepire un suono risultante. Ciò significa che ogni nota possiede fisicamente dentro di sé altre note, ma in dosaggi differenti. Ad esempio in un DO si trovano tanti SOL e MI (che originano la triade maggiore), ma anche SIb sebbene in misura ridotta, e anche RE in misura ancora minore.

Gli armonici hanno frequenze che sono multipli interi delle frequenze della nota fondamentale, ciò implica che il rapporto tra i numeri d’ordine dei vari suoni armonici corrisponde esattamente al rapporto esistente tra le loro frequenze. Es. il rapporto fra il DO2 e DO1 è 2⁄1, infatti la frequenza è doppia nella nota all’ottava superiore. Fra SOL3 e SOL2 il rapporto è 6⁄3, ancora frequenza doppia. Il rapporto tra SOL2 e DO2 (distanza di quinta) è 3⁄2, come facilmente evincibile dalle figure 1 e 2.
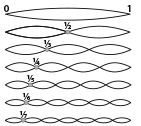
TEMPO E RITMO
Il tempo di un brano, identificato dalla frazione posta accanto alla chiave all’inizio dello spartito, indica la grandezza di ciascuna battuta del brano stesso. Si differenzia dal ritmo che è tutt’altra cosa, ossia la successione dei diversi valori (durate) delle note di un pezzo. Il tempo ci dà però anche un’altra importantissima informazione, ossia quanti accenti ritmici vi sono in una battuta (lo spazio tra 2 stanghette verticali).
In matematica posso semplificare la frazione 4⁄4 in 2⁄2 in quanto equivalenti; viceversa in musica l’equivalenza decade perché nel primo caso avremo 4 accenti per battuta, nel secondo solamente 2. E ancora 6⁄8 si semplifica matematicamente in 3⁄4 ma in musica nel primo caso avremo 2 accenti, mentre nel secondo 3.
La nostra percezione fisiologica del tempo si rifà a 3 suddivisioni fondamentali: 2, 3 e 4. Qualsiasi tempo più grande viene ricondotto sempre al più semplice di questi 3 schemi. Dunque come assimiliamo noi un tempo di 6⁄8? Dividendolo inconsciamente in 3+3, quindi in 2 gruppi accentuativi principali (schema del 2). Ecco spiegato perché il 6⁄8 si rifà allo schema del 2. Come assimiliamo il 12⁄8? Dividendolo in 3+3+3+3, quindi in 4 gruppi accentuativi (schema del 4). Anche un tempo irregolare come il 5⁄4, assai usato nella musica jazz, viene percepito come raggruppamento di 2+3 oppure 3+2, a seconda della posizione degli accenti scelta dal compositore.
FORMA
Nella musica, la forma svolge da sempre un ruolo essenziale. Ogni brano è, nei fatti, un percorso, un viaggio, costituito da innumerevoli articolazioni, nel quale ci si allontana più o meno da “casa” e si percorrono sia strade nuove sia strade già note. Quelle nuove contribuiscono a stimolare la curiosità e ci invogliano a continuare il viaggio; quelle già note però ci permettono di mantenere dei punti saldi di riferimento, per non smarrirci. Vi è dunque una continua alternanza tra fasi espansive (con tendenza al nuovo, ad allontanarsi) e fasi distensive (con tendenza a ritornare su percorsi noti). La forma serve a gestire queste due componenti nel modo più efficace possibile, affinché lo slancio verso il nuovo e la tensione verso “casa” siano opportunamente bilanciati.
Parlando delle parti in cui viene suddiviso un brano (macrostruttura), ci sono schemi formali che hanno dato da secoli prova della loro efficacia:
- A–A1: dove ad una prima parte espositiva delle idee musicali (A) segue una seconda (A1) che, pur ripercorrendole, le varia fornendoci uno stimolo;
- A–B–A: dove l’idea iniziale A si alterna ad una totalmente nuova B, prima della ripresentazione finale già nota di A;
- A–B–A–C–A–D–A… ovvero il rondò (circolo), dove l’idea iniziale A viene ripetutamente utilizzata in alternanza a idee sempre variate e diverse B, C, D… ecc. Questa struttura tipica del XVIII-XIX secolo è, se ci pensiamo bene, quella adottata dalle nostre moderne canzoni, costruite sull’alternanza tra ritornello (sempre uguale) e strofe (differenziate fra loro).
Considerando ora invece la microstruttura di un brano, ovvero le articolazioni interne ad una parte macrostrutturale (ad esempio le articolazioni interne ad A), scopriamo che la musica è davvero assimilabile ad un linguaggio, poiché come esso si presenta suddivisa in periodi, frasi, semifrasi, incisi e piedi. Il piede è la più piccola unità ritmica che indica in modo compiuto il movimento (in letteratura costituito da almeno 2 sillabe). Può corrispondere a mezza battuta, talvolta anche meno. Classicamente 2 piedi formano un inciso, 2 incisi una semifrase, 2 semifrasi una frase e 2 frasi un periodo. Ma naturalmente nella storia della musica esistono anche periodi irregolari formati da un numero variabile di frasi, incisi e piedi che ne aumentano la carica drammatica.
RIPETIZIONE E SIMMETRIA
Da un punto di vista estetico, la ripetizione è un classico canone di bellezza. La ripetizione tuttavia non deve rimanere sempre uguale a se stessa, altrimenti a lungo andare provocherebbe una sensazione di noia. Essa al contrario deve sempre essere innovata mediante piccole ‘variazioni sul tema’. Questi minuti e continui cambiamenti nella copia di un modello comune catturano lo spettatore, che si ritrova sempre stimolato dalle novità introdotte pur restando sempre in un contesto già noto. La natura ci offre molti modelli che si ispirano a questo paradigma: una fiamma ardente, i fiocchi di neve, il broccolo romanesco, la felce (fig. 3). Anche nell’arte si segue lo stesso paradigma.

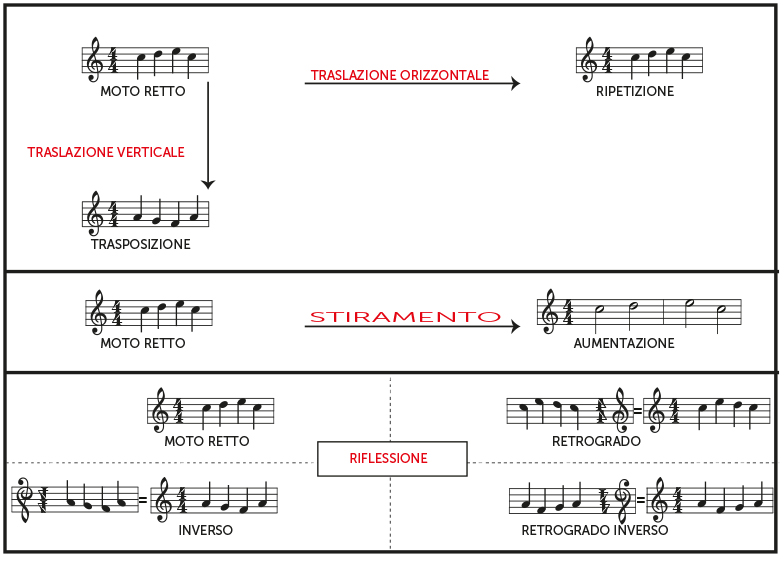
Ripetizione e simmetria sono concetti utilizzati ampiamente anche in musica. Lo spartito musicale infatti può essere considerato alla stregua di un grafico matematico in cui l’asse delle ascisse rappresenta il tempo e l’asse delle ordinate indica la frequenza (altezza) delle note. Ecco in fig. 5 come le trasformazioni sopra descritte si possono applicare ad uno spartito (in questo caso la prima battuta di Fra Martino).
La forma musicale che sfrutta maggiormente queste trasformazioni si chiama Canone (dal greco Kanon = legge o regola). Il canone più famoso (e semplice) è senza dubbio il già citato Fra Martino; si tratta di una canzone popolare francese del XVIII sec. attribuita a Jean Philippe Rameau in cui la voce principale viene ripetuta ad intervalli costanti. Altro esempio, famoso in quanto utilizzato spesso come colonna sonora dei matrimoni, è il Canone del religioso e musicista tedesco Johann Pachelbel (XVII sec.).
JOHANN SEBASTIAN BACH (1685-1750)
Colui che ha utilizzato queste trasformazioni con grande maestria è stato Johann Sebastian Bach, compositore e musicista tedesco del periodo barocco. Bach aveva una particolare predilezione per il numero 14: se si fa corrispondere ad ogni lettera dell’alfabeto1 un numero progressivo (A=1, B=2, C=3, ecc.) secondo il procedimento chiamato gematria, si vede che le lettere B-A-C-H corrispondono ai numeri 2-1-3-8, la cui somma vale 14. Se alle lettere BACH si aggiungono anche le iniziali JS, si ottiene 41 che è lo speculare di 14. Elenchiamo ora alcune notevoli opere di Bach costruite matematicamente.
Il tema dell’aria iniziale delle Variazioni Goldberg (BWV 988, 1741-1745) consta, una volta depurato dagli abbellimenti, di 14 note. Le Variazioni comprendono: 1 (=A) aria, 3 (=C) variazioni in minore e 28 pezzi rimanenti (2=B e 8=H): ridistribuendo le lettere troviamo ancora BACH.
Nell’Arte della Fuga (BWV 1080, 1740-1750) sono presenti 14 contrappunti, di cui 2 (=B) fughe a specchio, 1 (=A) grande fuga, 3 (=C) fughe a imitazione e 8 (=H) fughe semplici doppie e triple, ancora BACH. Applicando la gematria al titolo originale tedesco “Die Kunst der Fuga”2 si ottiene il numero 158, lo stesso numero che si ottiene applicando la gematria al nome completo “Johann Sebastian Bach”. E ovviamente 1+5+8=143!!! Di mirabile costruzione risulta il Contrapunctus VII a 4 voci per aumentazione e diminuzione: al suo interno Bach riuscì ad inserire ben 28 (il doppio di 14) ripetizioni del tema principale, usando 16 moti retti e 12 moti contrari, con aumentazione e diminuzione.
L’Offerta Musicale (BWV 1079, 1747) fu scritta da Bach in onore del re Federico II di Prussia, grande appassionato di musica e suonatore dilettante di flauto. Il re invitò Bach a palazzo e gli fece provare i suoi innumerevoli clavicembali, Bach per ringraziarlo gli chiese un tema su cui improvvisare una fuga a 3 voci, cosa che fece puntualmente nonostante il tema proposto fosse piuttosto complicato. Il re allora lo volle sfidare ulteriormente chiedendogli di improvvisare una fuga a 6 voci sullo stesso tema, Bach riuscì nell’impresa usando un tema semplificato e si ripropose di spedire successivamente al re la fuga sul tema completo. Alla fine, oltre alla fuga, Bach aggiunse altri 12 pezzi, tutti dedicati al re. Di particolare interesse risulta il cosiddetto Canone Cancrizzante, che può essere suonato in contemporanea partendo dall’inizio (moto retto) e partendo dalla fine (moto retrogrado).

Nel gennaio 1974, nella terza pagina di copertina di una stampa originale delle Variazioni Goldberg, venne ritrovato un foglio manoscritto che, dopo perizie tecniche e calligrafiche, fu attribuito senza ombra di dubbio a Bach. Si trattava di 14 Canoni sulle prime 8 note del basso Goldberg (BWV 1087, 1747). Bach li compose per motivi di analisi e di speculazione teorico-matematica. Tutti i canoni trovano spazio in un’unica facciata perché sono trascritti in modo ‘enigmatico’, nel senso che Bach ha scritto soltanto la voce principale mentre tutte le altre sono solo abbozzate usando dei simboli particolari che vanno ovviamente decifrati. Una specie di Settimana Enigmistica ante litteram. In questa sede citiamo soltanto il Canon Duplex a 4 voci, che prevede una parte principale (moto retto) coesistente esattamente con la sua riflessa rispetto ad un asse orizzontale (moto inverso).
Bach non ha scritto alcun pezzo che possegga interamente la trasformazione retrograda inversa. In generale questa tipologia di canone è molto rara, poiché la sua costruzione risulta particolarmente ostica. A causa del fatto che le due trasformazioni (riflessione sia sull’asse orizzontale che sull’asse verticale) corrispondono ad una rotazione di 180°, questi canoni sono anche detti canoni al tavolo perché possono essere suonati contemporaneamente da due esecutori disposti uno di fronte all’altro ai due estremi di un tavolo leggendo lo stesso spartito. L’esempio più famoso è il Canone a Specchio, di origine incerta ma attribuito probabilmente a Mozart.
FRANCESCO GIOIA, GIULIO PRAVISANI
[1] Al lettore curioso, che volesse cimentarsi con i conti, segnaliamo (senza addentrarci in motivazioni storiche) che questo alfabeto vede come “intercambiabili” le lettere “i” e “j”, che pertanto riceveranno lo stesso valore numerico (9). ⇑
[2] Questa forma del titolo è tratta dal Mus. ms. Bach P 200. ⇑
[3] Se le strutture matematiche utilizzate da Bach sono ineccepibili, è opportuno ricordare che queste coincidenze numerologiche, per quanto suggestive, vanno comunque valutate sotto un profilo più ludico che scientifico. ⇑
